
1편과 이어서 Transformer에 대해서 설명드리겠습니다. 이전에 Transformer의 구조를 한번더 복습하고 진행하겠습니다.
1. Transformer의 structure 보기

input Embedding과 Positional Encoding 층을 지나면 Attention을 만나볼 수 있는데요. 트랜스포머의 인코더와 디코더에서 사용하고 있는 개념인 어텐션에 대해서 알아보겠습니다. (Attention의 등장 배경과 짧은 설명은 transformer 1편에 설명되어 있습니다.)
2. 트랜스포머에서 사용된 Attention


트랜스포머는 총 세 가지의 어텐션이 사용되는데요, 세가지 어텐션에 대해서 간단히 정리해 보면 아래와 같습니다.
- Encoder Self-Attention
- decoder Masked Self-Attention
- decoder Encoder-Decoder Attention
Attention은 입력데이터의 특정 부분에 집중한다고 하였습니다. 집중이라는 것은 각 단어가 어떤 단어들과 관련있는지에 유사도에 대한 것을 말하는데요, 그렇다면 각 Attention의 이름을 보면 각 Attention이 어떤 부분에 집중하고 있는지 힌트를 얻을 수 있습니다. 우측에 있는 사진과 함께 보며 대략적으로 이해해봅시다.
Encoder Self-Attention : encoder의 입력으로 들어온 문장을 서로 비교하여 관련도를 찾습니다.
Decoder Masked Self-Attention : decoder는 문장을 생성하는데요, 미래에 출력될 부분을 참조하지 않고 이미 출력된 부분들만 참조하여 관련도를 찾는다는 의미로 볼 수 있습니다.
Decoder Encoder-Decoder Attention: decoder가 다음문장을 예측하기 위해, encoder 부분에 입력된 단어들의 유사도를 구해서 참조합니다.
이중 두가지에 Self-Attention이 쓰인 것을 볼 수 있는데요. Self-Attention에 대해서 알아봅시다.
3. 셀프 어텐션(Self Attention)
Self Attention에 대해 알아봅시다.

“The animal didn't cross the street becasue it was too tired” 라는 문장이 있을때, it 이 의미하는 것은 뭘까요.
사람에게는 animal 이라는 것이 너무 간단한 문제이지만, 모델에게는 쉬운 문제는 아닙니다. 모델이 “it”이라는 단어를 처리할 때, 모델은 self-attention 을 이용하여 단어들의 관계성을 파악하고, “it”과 “animal”을 연결시킬 수 있습니다.
3-1) Self Attention 출력값 계산하기
self attention의 첫번째 단계는 Embedding vector로부터 Query, Key, Value 벡터를 생성하는 것 입니다.
(1)Query, Key, Value 벡터 생성
I am good 라는 문장이 input으로 들어온다면, 첫 번째로 각 단어를 embeding 처리 합니다. 이후 W과 내적하여 Query, Key, Value값을 얻을 수 있는데요. 문장의 첫번째 단어인 I 가 X라는 임베딩 벡터로 가정한다면, 아래와 같이 Query, Key, Value 값을 얻을 수 있겠네요.
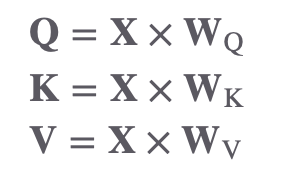
- X를 WQ와 내적하여 query 벡터인 q1을 생성합니다.
- X를 WK와 내적하여 key 벡터인 k1을 생성합니다.
- X를 WV와 내적하여 value 벡터인 v1을 생성합니다.
자 위의 과정을 한번 행렬곱으로 확인 해 봅시다.
Query 만들기
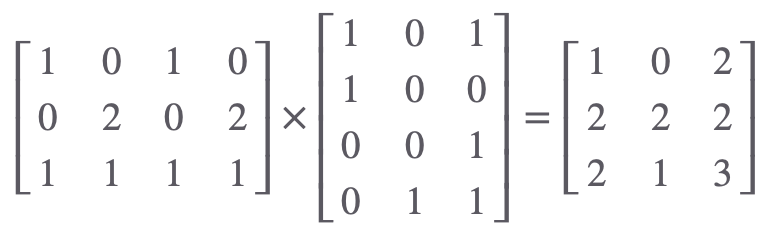
I am good 이라는 단어를 embedding 해서 아래와 같은 벡터로 변환한다고 가정해봅시다.
I → [1010]
am → [0202]
good → [1111]
행렬곱 연산으로 각 단어에 대한 Query 값을 구할 수 있겠네요.
I → [102]
am → [222]
good → [213]
그럼 이어서 Key와 Value값도 구해보겠습니다.
Key 만들기
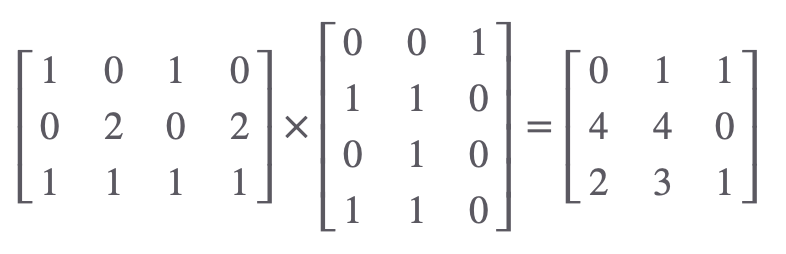
행렬곱 연산으로 각 단어에 대한 Key 값을 구할 수 있겠네요.
I → [011]
am → [440]
good → [231]
value 만들기
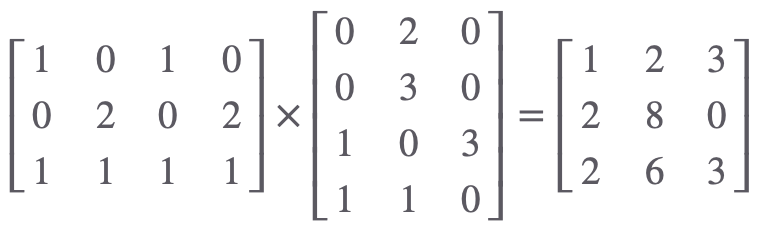
I → [123]
am → [280]
good → [263]
다음으로 우리가 할 일은 셀프 어텐션 출력값 계산하기 입니다. 이제 우리가 만든 Query, Key, Value값이 빛을 발할 때가 왔습니다. 우선 셀프 어텐션 값의 정의를 보고 갈까요?
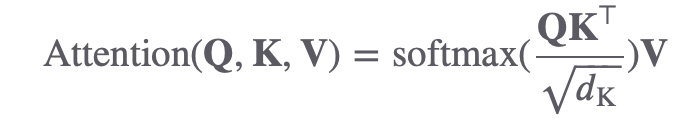
수식을 말로 풀면,
(1)쿼리와 키를 행렬곱한 뒤 해당 행렬의 모든 요소값을 (2)키 차원수의 제곱근 값으로 나눠주고, 이 행렬을 행 (3)(row) 단위로 소프트맥스(softmax)*를 취해 스코어 행렬을 만들어줍니다. 이 스코어 행렬에 (4)밸류를 행렬곱해 줘서 셀프 어텐션 계산을 마무리 합니다. 라고 할 수 있겠네요.
(2)첫번째 쿼리의 Self-Attention 출력값 계산하기
한번 셀프 어텐션 값을 구해볼까요?
우선 첫번째 쿼리를 한번 가져오겠습니다.
I → [102]
자, 여기서 Query의 역할이 나오는데요. Query는 검색창에 질문을 하는 것으로 생각할 수 있는데요. 차차 연산을 통해 왜 그런 역할인지 알아봅시다.
첫번째 시퀀스 I의 쿼리는 [102] 입니다. 여기에 모든 키값을 하나하나씩 곱하는 것인데요.
I am good에 대한 모든 Key값을 아래와 같습니다.
I → [011]
am → [440]
good → [231]
행렬곱을 이용해 모든 Key값을 Transpose하고 값을 구해봅시다.
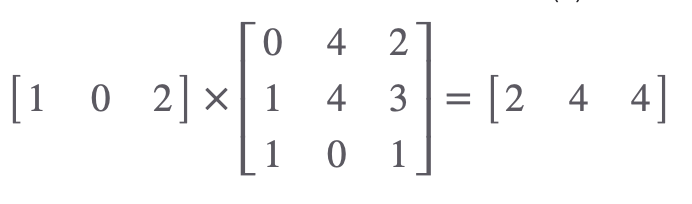
2, 4, 4 라는 숫자가 나왔습니다. 각 요소의 의미를 살펴보면 아래와 같겠네요.
2 → 첫번째 쿼리와 첫번째 키 값의 결과
4 → 두번째 쿼리와 두번째 키 값의 결과
4 → 세번째 쿼리와 세번째 키 값의 결과
여기서 2, 4, 4가 의미하는 바는 바로, 첫번째 Query와 다른 시퀀스들의 문맥적 관계성을 표현한 것입니다. 숫자가 높을 수록 더 높은 관계를 갖는다는 것을 예상할 수 있습니다.
정리하면, 첫번째 시퀀스에 대한 Query와 모든 시퀀스의 Key값을 행렬곱한 결과 2, 4, 4는 첫번째 단어 I 와 I , am, good 이라는 단어들에 대한 관계성을 나타낸다고 볼 수 있습니다. 끝이 아닙니다.
2, 4, 4에 대해 키 벡터의 차원의 수(3)의 제곱근으로 나눈 후 Softmax를 취해주어야 하는데요. 그결과는 아래에 있습니다.
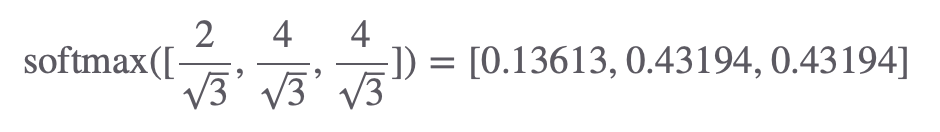
[0.13613, 0.43194, 0.43194] 는 아래와 같은 순서로 나온 결과입니다.
1. 첫번째 단어 I 에 대한 Query 값을 I / am / good 모든 각각의 단어의 Key 값을 곱했음 -> 단어들에 대한 관계성
2. 나온 결과 [2, 4, 4]에 키벡터의 차원수의 제곱근으로 나눠주고, Softmax를 취해줬음
Softmax는 곱셈 결과를 0과 1 사이의 값으로 변환하는 역할로 2, 4, 4가 각각 확률 값으로 나오게 됩니다. 즉 첫 번째 단어가 문장 내 다른 모든 단어들과 얼마나 관련 있는지를 나타내는 확률 분포로 확인할 수 있습니다.
각각 첫번째 Query와 첫번째 단어의 관련도, 첫번째 Query와 두번째 단어의 관련도, 첫번째 Query와 세번째 단어의 관련도에 대한 확률이라고 볼 수 있겠네요.
여기서 키벡터의 차원수의 제곱근으로 나눠주는 이유는 계산의 안정성을 위해서입니다.
이제 마지막 연산입니다.
첫 번째 단어가 문장 내 다른 모든 단어들과 얼마나 관련 있는지를 나타내는 확률 분포인 [0.13613, 0.43194, 0.43194] 값을, 벨류벡터와 weighted sum을 해야하는데요.
우선 아까 구했던 Value값을 가져옵니다.
I → [123]
am → [280]
good → [263]
첫 번째 단어가 문장 내 다른 모든 단어들과 얼마나 관련 있는지를 나타내는 확률 분포인 [0.13613,0.43194,0.43194] 값과 I /am / good 에 해당하는 Value 벡터와 곱해준 후 더해줍니다.
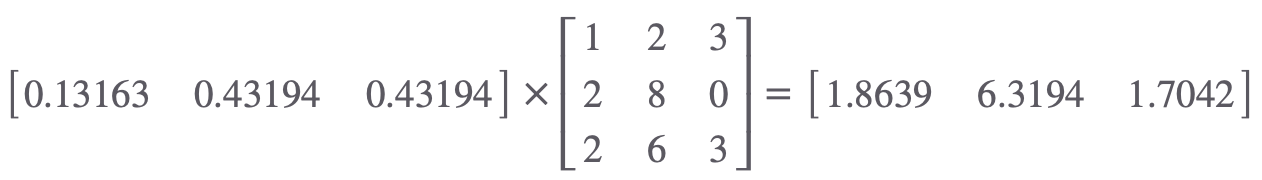
- 첫번째 단어가 첫번째 단어와 얼마나 관련있는지 해당하는 0.13613과 첫번째 단어의 Value값의 곱의 합입니다.
- 두번째 단어가 두번째 단어와 얼마나 관련있는지 해당하는 0.43194과 두번째 단어의 Value값의 곱의 합입니다.
- 세번째 단어가 세번째 단어와 얼마나 관련있는지 해당하는 0.43194 세번째 단어의 Value값의 곱의 합입니다.
나온 결과인 [1.9991 7.8141 0.2735]가 첫번째 단어 I 의 쿼리 벡터에 대한 SelfAttention 결과입니다.
즉, 첫번째 단어가 첫번째 단어와, 두번째 단어, 세번째 단어와 얼마나 관계성을 가졌는지 알 수 있겠네요.
(3)두번째 쿼리의 Self-Attention 출력값 계산하기
두번째 시퀀스의 Query 값과 모든 Key값을 행렬곱 해줍니다. 두번째 Query와 다른 시퀀스들의 문맥적 관계성을 표현한 것입니다.
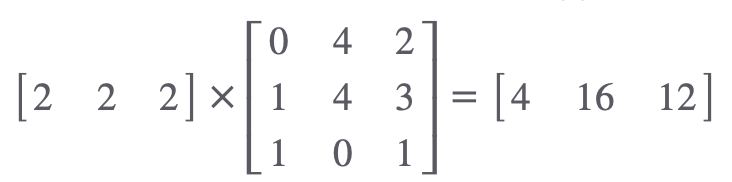
키 벡터의 차원의 수(3)의 제곱근으로 나눈 후 Softmax를 취해줍니다. 두 번째 단어가 문장 내 다른 모든 단어들과 얼마나 관련 있는지를 나타내는 확률 분포를 나타냅니다.
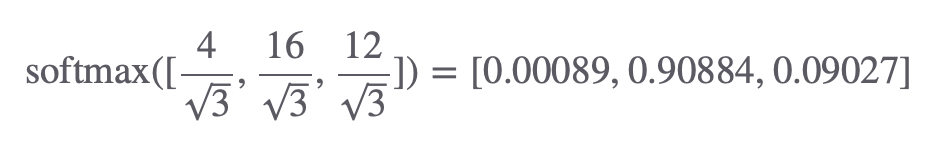
나온 결과를 각각에 해당하는 Value 벡터와 곱해줍니다. 각각 두번째 Query와 첫번째 단어의 관련도, 두번째 Query와 두번째 단어의 관련도, 첫번째 Query와 세번째 단어의 관련도에 대한 확률이라고 볼 수 있겠네요.
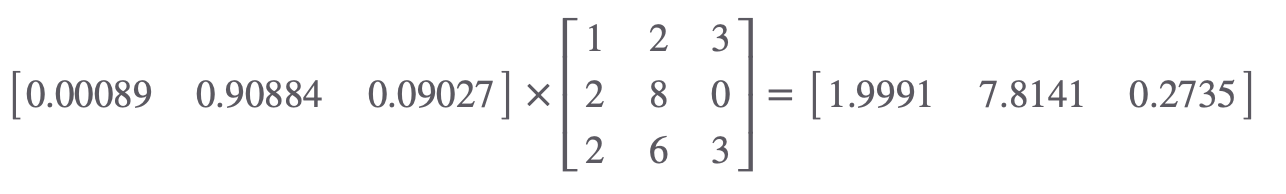
두번째 단어 am 의 쿼리 벡터에 대한 SelfAttention 결과입니다.
이와 같이 모든 단어의 Query 에대한 SelfAttention 결과를 낼 수 있습니다. SelfAttention안에는 각 단어가 다른 단어와의 관계를 나타낼 수 있습니다.
다시 위로 올라가서 “The animal didn't cross the street becasue it was too tired” 라는 단어에 SelfAttention 결과값을 낸다면, 뒤에 나오는 It이라는 단어가 animal 이라는 단어에 연관도가 높다는 것을 알수있게 모델이 훈련된다면 더욱 훌륭한 모델이 되겠네요.
(4)그림으로 살펴보기
아래 내용은 I study at school 라는 문장에 대한 SelfAttention 과정을 그림으로 나타내면 아래와 같습니다.

지금까지의 연산 과정을 정리하면 위 사진으로 표현할 수 있습니다. 정리하면,
- 첫번째 Query와 모든 Key 값을 곱해줍니다. 나오는 모든 값을 softmax 처리하게 되면 Key값에 해당하는 단어가 현재 Query 단어 에 어느정도 연관성이 있는지 나타냅니다.(예를 들어 I는 자기자신과 92% 나머지는 0.05, 0.02, 0.01 연관성이 있다고 나옴)
- 나온 결과들에 각 키에 해당하는 value를 곱해주면 연관성이 없는 value값은 희미해집니다. 최종적으로 Attention이 적용되어 희미해진 value들을 모두 더해주는데, 최종 벡터는 단순 단어 I가 아닌 문장속에서 단어 I 가 지닌 전체적인 의미를 지닌 vector로 간주할 수 있습니다.
reference
- https://ratsgo.github.io/nlpbook/docs/language_model/tr_self_attention/
'AI' 카테고리의 다른 글
| 생물학적 뉴런과 인공 신경망 (1) | 2024.07.03 |
|---|---|
| Transformer (Multi-head Attention) (0) | 2024.06.22 |
| Transformer - Structure, Posititonal Encoding (0) | 2024.06.20 |
| LSTM의 Cell State와 Gate별 특징 (0) | 2024.06.19 |
| RNN(Recurrent Neural Networks) (1) | 2024.06.19 |



